Wenn es umAntennenDie Frage, die die Menschen am meisten beschäftigt, lautet: „Wie wird Strahlung eigentlich erzeugt?“ Wie breitet sich das von der Signalquelle erzeugte elektromagnetische Feld durch die Übertragungsleitung und im Inneren der Antenne aus und „trennt“ sich schließlich von der Antenne, um eine Freiraumwelle zu bilden?
1. Einzeldrahtstrahlung
Nehmen wir an, dass die Ladungsdichte, ausgedrückt als qv (Coulomb/m3), gleichmäßig in einem kreisförmigen Draht mit einer Querschnittsfläche von a und einem Volumen von V verteilt ist, wie in Abbildung 1 dargestellt.
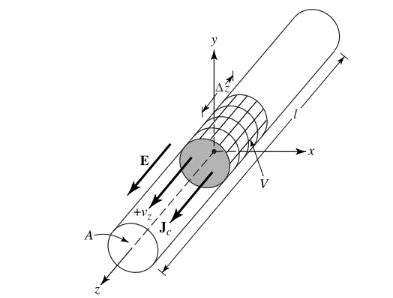
Abbildung 1
Die Gesamtladung Q im Volumen V bewegt sich mit der gleichmäßigen Geschwindigkeit Vz (m/s) in z-Richtung. Es lässt sich beweisen, dass die Stromdichte Jz im Querschnitt des Drahtes beträgt:
Jz = qv vz (1)
Besteht der Draht aus einem idealen Leiter, so beträgt die Stromdichte Js an der Drahtoberfläche:
Js = qs vz (2)
Dabei ist qs die Oberflächenladungsdichte. Ist der Draht sehr dünn (idealerweise beträgt der Radius 0), lässt sich der Strom im Draht wie folgt ausdrücken:
Iz = ql vz (3)
Hierbei ist ql (Coulomb/Meter) die Ladung pro Längeneinheit.
Wir befassen uns hauptsächlich mit dünnen Drähten, und die Schlussfolgerungen gelten für die drei oben genannten Fälle. Wenn der Strom zeitlich veränderlich ist, lautet die Ableitung der Formel (3) nach der Zeit wie folgt:
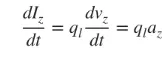
(4)
az ist die Ladungsbeschleunigung. Wenn die Drahtlänge l beträgt, kann (4) wie folgt geschrieben werden:
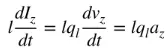
(5)
Gleichung (5) beschreibt den grundlegenden Zusammenhang zwischen Stromstärke und Ladung sowie die grundlegende Beziehung elektromagnetischer Strahlung. Vereinfacht gesagt: Um Strahlung zu erzeugen, muss ein zeitlich veränderlicher Strom oder eine Beschleunigung (bzw. Verzögerung) der Ladung vorliegen. Stromstärke wird üblicherweise bei zeitlich harmonischen Anwendungen betrachtet, Ladung hingegen meist bei transienten Anwendungen. Um eine Ladungsbeschleunigung (bzw. -verzögerung) zu erzeugen, muss der Draht gebogen, gefaltet oder diskontinuierlich sein. Schwingt die Ladung in einer zeitlich harmonischen Bewegung, so erzeugt sie ebenfalls eine periodische Ladungsbeschleunigung (bzw. -verzögerung) oder einen zeitlich veränderlichen Strom. Daher gilt:
1) Wenn sich die Ladung nicht bewegt, fließt kein Strom und es findet keine Strahlung statt.
2) Wenn sich die Ladung mit konstanter Geschwindigkeit bewegt:
a. Wenn der Draht gerade und unendlich lang ist, gibt es keine Strahlung.
b. Wenn der Draht gebogen, gefaltet oder unterbrochen ist, wie in Abbildung 2 dargestellt, entsteht Strahlung.
3) Wenn die Ladung mit der Zeit oszilliert, strahlt die Ladung auch dann ab, wenn der Draht gerade ist.
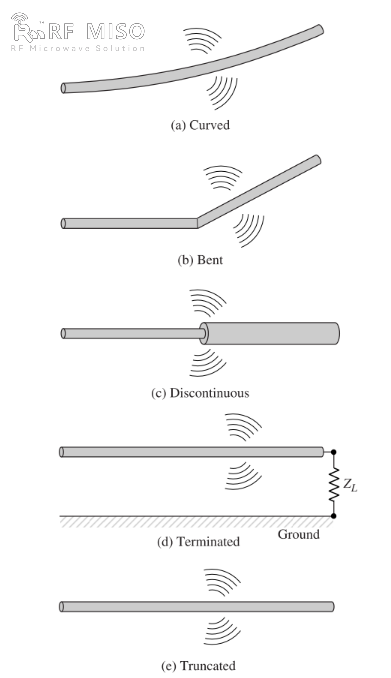
Abbildung 2
Ein qualitatives Verständnis des Strahlungsmechanismus lässt sich anhand einer gepulsten Quelle gewinnen, die an einen offenen Draht angeschlossen ist, dessen offenes Ende über eine Last geerdet werden kann (siehe Abbildung 2(d)). Beim ersten Anlegen einer Spannung an den Draht werden die Ladungen (freie Elektronen) im Draht durch die von der Quelle erzeugten elektrischen Feldlinien in Bewegung gesetzt. Da die Ladungen am Quellende des Drahtes beschleunigt und beim Reflektieren am anderen Ende abgebremst werden (negative Beschleunigung relativ zur ursprünglichen Bewegung), entsteht an den Enden und entlang des restlichen Drahtes ein Strahlungsfeld. Die Beschleunigung der Ladungen erfolgt durch eine äußere Kraftquelle, die die Ladungen in Bewegung setzt und das zugehörige Strahlungsfeld erzeugt. Die Abbremsung der Ladungen an den Drahtenden wird durch innere Kräfte bewirkt, die mit dem induzierten Feld verbunden sind. Dieses Feld entsteht durch die Ansammlung konzentrierter Ladungen an den Drahtenden. Die inneren Kräfte gewinnen Energie aus der Ladungsansammlung, da deren Geschwindigkeit an den Drahtenden auf null abnimmt. Die Beschleunigung von Ladungen durch die elektrische Feldanregung und die Verzögerung von Ladungen aufgrund von Unstetigkeiten oder Krümmungen der Drahtimpedanz sind die Mechanismen zur Erzeugung elektromagnetischer Strahlung. Obwohl sowohl Stromdichte (Jc) als auch Ladungsdichte (qv) Quellterme in den Maxwell-Gleichungen sind, gilt die Ladung als fundamentalere Größe, insbesondere bei transienten Feldern. Diese Erklärung der Strahlung wird zwar hauptsächlich für transiente Zustände verwendet, kann aber auch zur Erklärung stationärer Strahlung herangezogen werden.
Empfehlen Sie mehrere ausgezeichneteAntennenproduktehergestellt vonRFMISO:
2. Zweidrahtstrahlung
Schließen Sie eine Spannungsquelle an eine Zweileiter-Übertragungsleitung an, die mit einer Antenne verbunden ist (siehe Abbildung 3(a)). Durch Anlegen einer Spannung an die Zweileiterleitung entsteht ein elektrisches Feld zwischen den Leitern. Die Feldlinien wirken auf die freien Elektronen (die sich leicht von Atomen trennen lassen), die mit jedem Leiter verbunden sind, und versetzen sie in Bewegung. Die Bewegung der Ladungen erzeugt einen Strom, der wiederum ein Magnetfeld erzeugt.
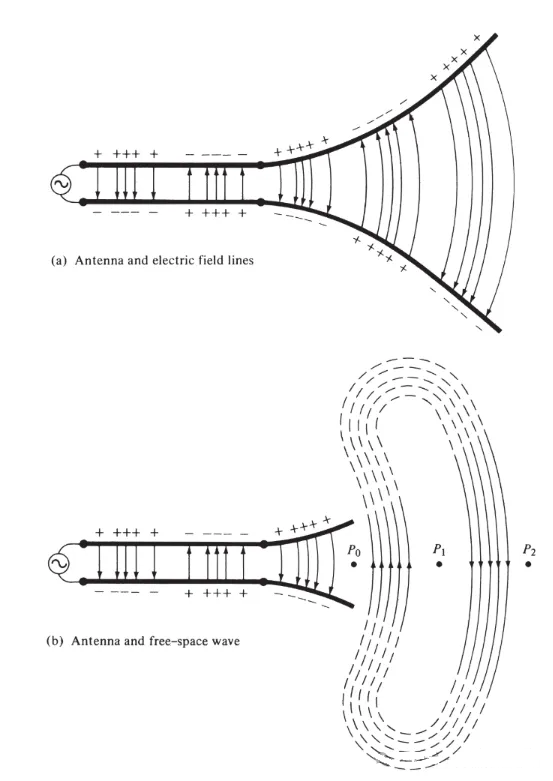
Abbildung 3
Wir haben akzeptiert, dass elektrische Feldlinien mit positiven Ladungen beginnen und mit negativen Ladungen enden. Natürlich können sie auch mit positiven Ladungen beginnen und im Unendlichen enden; oder im Unendlichen beginnen und mit negativen Ladungen enden; oder geschlossene Schleifen bilden, die weder mit Ladungen beginnen noch enden. Magnetische Feldlinien bilden stets geschlossene Schleifen um stromdurchflossene Leiter, da es in der Physik keine magnetischen Ladungen gibt. In einigen mathematischen Formeln werden äquivalente magnetische Ladungen und magnetische Ströme eingeführt, um die Dualität zwischen Lösungen mit Leistungs- und Magnetquellen aufzuzeigen.
Die zwischen zwei Leitern eingezeichneten elektrischen Feldlinien veranschaulichen die Ladungsverteilung. Geht man von einer sinusförmigen Spannungsquelle aus, so ist auch das elektrische Feld zwischen den Leitern sinusförmig mit einer Periode gleich der der Quelle. Die relative Stärke des elektrischen Feldes wird durch die Dichte der Feldlinien dargestellt, die Pfeile geben die relative Richtung (positiv oder negativ) an. Die Erzeugung zeitlich veränderlicher elektrischer und magnetischer Felder zwischen den Leitern erzeugt eine elektromagnetische Welle, die sich entlang der Übertragungsleitung ausbreitet (siehe Abb. 3(a)). Die elektromagnetische Welle tritt mit der Ladung und dem entsprechenden Strom in die Antenne ein. Entfernt man einen Teil der Antennenstruktur (siehe Abb. 3(b)), so entsteht eine Freiraumwelle, indem die offenen Enden der elektrischen Feldlinien (gestrichelte Linien) verbunden werden. Auch die Freiraumwelle ist periodisch, jedoch bewegt sich der Punkt konstanter Phase P0 mit Lichtgeschwindigkeit nach außen und legt in einer halben Periode eine Strecke von λ/2 (bis P1) zurück. In der Nähe der Antenne bewegt sich der Punkt konstanter Phase P0 schneller als mit Lichtgeschwindigkeit und nähert sich dieser in größerer Entfernung von der Antenne an. Abbildung 4 zeigt die elektrische Feldverteilung im freien Raum der λ/2-Antenne zu den Zeitpunkten t = 0, t/8, t/4 und 3T/8.
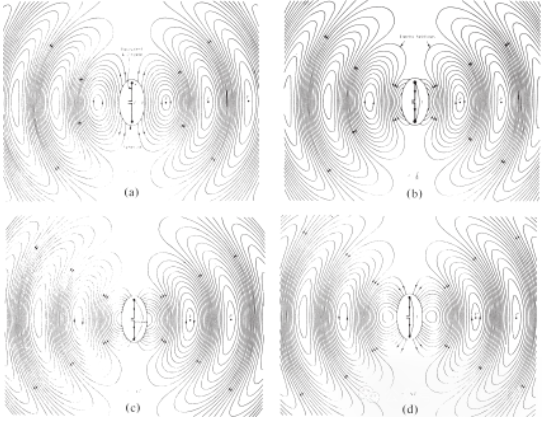
Abbildung 4: Elektrische Feldverteilung im freien Raum der λ/2-Antenne bei t = 0, t/8, t/4 und 3T/8
Es ist nicht bekannt, wie die geführten Wellen von der Antenne abgetrennt werden und sich schließlich im freien Raum ausbreiten. Man kann geführte und freie Wellen mit Wasserwellen vergleichen, die beispielsweise durch einen in ein ruhiges Gewässer geworfenen Stein oder auf andere Weise entstehen können. Sobald eine Störung im Wasser auftritt, werden Wasserwellen erzeugt und breiten sich aus. Selbst wenn die Störung aufhört, setzen sich die Wellen fort. Hält die Störung an, werden ständig neue Wellen erzeugt, deren Ausbreitung hinter der der anderen Wellen zurückbleibt.
Dasselbe gilt für elektromagnetische Wellen, die durch elektrische Störungen erzeugt werden. Ist die anfängliche elektrische Störung von der Quelle nur von kurzer Dauer, breiten sich die erzeugten elektromagnetischen Wellen in der Übertragungsleitung aus, treten in die Antenne ein und strahlen schließlich als Freiraumwellen ab, obwohl die Anregung nicht mehr vorhanden ist (ähnlich wie bei Wasserwellen und der von ihnen erzeugten Störung). Ist die elektrische Störung kontinuierlich, existieren die elektromagnetischen Wellen kontinuierlich und folgen ihr während der Ausbreitung dicht, wie in der bikonischen Antenne in Abbildung 5 dargestellt. Befinden sich elektromagnetische Wellen in Übertragungsleitungen und Antennen, hängt ihre Existenz von der elektrischen Ladung im Leiter ab. Werden die Wellen jedoch abgestrahlt, bilden sie einen geschlossenen Kreis, und es ist keine Ladung vorhanden, die ihre Existenz aufrechterhält. Daraus lässt sich schließen:
Zur Anregung des Feldes ist eine Beschleunigung und Verzögerung der Ladung erforderlich, zur Aufrechterhaltung des Feldes hingegen nicht.
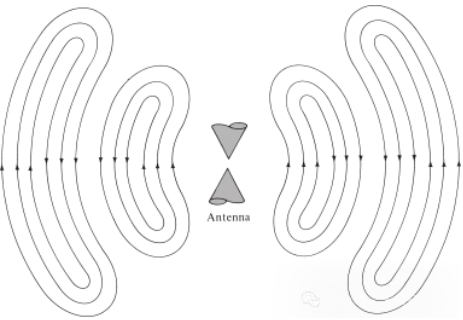
Abbildung 5
3. Dipolstrahlung
Wir versuchen, den Mechanismus zu erklären, durch den sich die elektrischen Feldlinien von der Antenne lösen und Freiraumwellen bilden, und verwenden die Dipolantenne als Beispiel. Obwohl es sich um eine vereinfachte Erklärung handelt, ermöglicht sie dennoch ein intuitives Verständnis der Freiraumwellenentstehung. Abbildung 6(a) zeigt die zwischen den beiden Armen des Dipols entstehenden elektrischen Feldlinien, wenn sich diese im ersten Viertel des Zyklus um λ/4 nach außen bewegen. Nehmen wir für dieses Beispiel an, dass drei elektrische Feldlinien entstehen. Im nächsten Viertel des Zyklus bewegen sich die ursprünglichen drei Feldlinien um weitere λ/4 (insgesamt λ/2 vom Ausgangspunkt), und die Ladungsdichte auf dem Leiter beginnt abzunehmen. Dies kann auf die Einführung entgegengesetzter Ladungen zurückgeführt werden, welche die Ladungen auf dem Leiter am Ende der ersten Zyklushälfte kompensieren. Die durch die entgegengesetzten Ladungen erzeugten drei elektrischen Feldlinien bewegen sich um die Strecke λ/4, was in Abbildung 6(b) durch die gestrichelten Linien dargestellt ist.
Das Endergebnis ist, dass sich im ersten λ/4-Abstand drei nach unten gerichtete elektrische Feldlinien und im zweiten λ/4-Abstand die gleiche Anzahl nach oben gerichteter elektrischer Feldlinien befindet. Da die Antenne keine Nettoladung trägt, müssen sich die elektrischen Feldlinien vom Leiter lösen und sich zu einer geschlossenen Schleife verbinden. Dies ist in Abbildung 6(c) dargestellt. In der zweiten Hälfte wiederholt sich der gleiche physikalische Prozess, jedoch in umgekehrter Richtung. Anschließend wiederholt sich der Prozess unbegrenzt und erzeugt eine elektrische Feldverteilung ähnlich der in Abbildung 4.
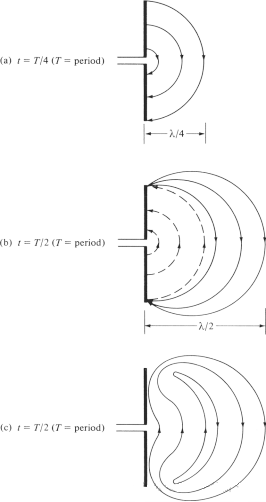
Abbildung 6
Um mehr über Antennen zu erfahren, besuchen Sie bitte:
Veröffentlichungsdatum: 20. Juni 2024










