Die Polarisation ist eine der grundlegenden Eigenschaften von Antennen. Zunächst müssen wir die Polarisation ebener Wellen verstehen. Anschließend können wir die wichtigsten Arten der Antennenpolarisation besprechen.
lineare Polarisation
Wir werden beginnen, die Polarisation einer ebenen elektromagnetischen Welle zu verstehen.
Eine ebene elektromagnetische Welle (EM-Welle) weist mehrere Eigenschaften auf. Erstens breitet sich die Energie nur in eine Richtung aus (das Feld ändert sich nicht in zwei orthogonalen Richtungen). Zweitens stehen das elektrische und das magnetische Feld senkrecht zueinander. Sie verlaufen senkrecht zur Ausbreitungsrichtung der ebenen Welle. Betrachten wir beispielsweise ein elektrisches Feld (E-Feld) mit einer einzigen Frequenz, gegeben durch Gleichung (1). Das elektromagnetische Feld breitet sich in +z-Richtung aus. Das elektrische Feld ist in +x-Richtung gerichtet. Das magnetische Feld ist in +y-Richtung gerichtet.
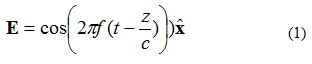
Beachten Sie in Gleichung (1) die Notation: . Dies ist ein Einheitsvektor (ein Vektor der Länge ), der besagt, dass der elektrische Feldpunkt in x-Richtung liegt. Die ebene Welle ist in Abbildung 1 dargestellt.
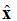
Abbildung 1. Grafische Darstellung des elektrischen Feldes in +z-Richtung.
Die Polarisation beschreibt die Spur und Ausbreitungsform (Kontur) eines elektrischen Feldes. Betrachten wir beispielsweise die Feldgleichung (1) für eine ebene Welle. Wir untersuchen die Position (X,Y,Z) = (0,0,0) des elektrischen Feldes als Funktion der Zeit. Die Amplitude dieses Feldes ist in Abbildung 2 zu verschiedenen Zeitpunkten dargestellt. Das Feld oszilliert mit der Frequenz „F“.
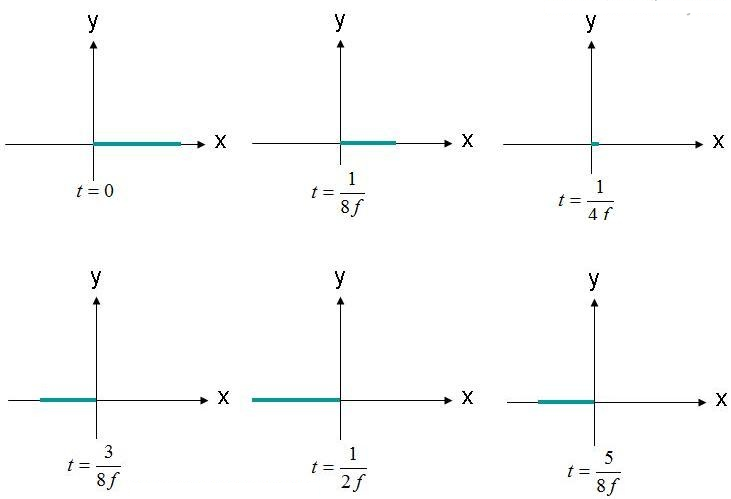
Abbildung 2. Beobachten Sie das elektrische Feld (X, Y, Z) = (0,0,0) zu verschiedenen Zeitpunkten.
Das elektrische Feld wird im Ursprung beobachtet und oszilliert in seiner Amplitude. Es verläuft stets entlang der angegebenen x-Achse. Da das elektrische Feld geradlinig verläuft, ist es linear polarisiert. Ist die x-Achse parallel zum Boden, spricht man zusätzlich von horizontaler Polarisation. Verläuft das Feld entlang der y-Achse, ist die Welle vertikal polarisiert.
Linear polarisierte Wellen müssen nicht entlang einer horizontalen oder vertikalen Achse ausgerichtet sein. Beispielsweise wäre eine elektrische Feldwelle, deren Ausbreitungsrichtung entlang einer Linie verläuft, wie in Abbildung 3 dargestellt, ebenfalls linear polarisiert.
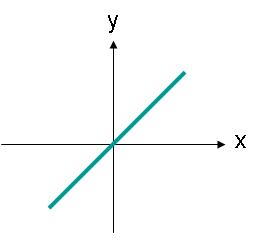
Abbildung 3. Die elektrische Feldamplitude einer linear polarisierten Welle, deren Trajektorie einen Winkel bildet.
Das elektrische Feld in Abbildung 3 lässt sich durch Gleichung (2) beschreiben. Es besitzt eine x- und eine y-Komponente. Beide Komponenten sind gleich groß.
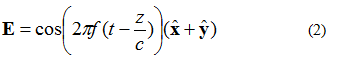
Eine Besonderheit von Gleichung (2) ist die xy-Komponente und das elektronische Feld in der zweiten Stufe. Dies bedeutet, dass beide Komponenten stets die gleiche Amplitude aufweisen.
Zirkularpolarisation
Nehmen wir nun an, dass das elektrische Feld einer ebenen Welle durch Gleichung (3) gegeben ist:
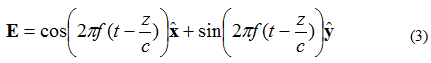
In diesem Fall sind die X- und Y-Elemente um 90 Grad phasenverschoben. Wenn das Feld wie zuvor wieder als (X, Y, Z) = (0,0,0) betrachtet wird, ergibt sich der in Abbildung 4 dargestellte Verlauf des elektrischen Feldes über der Zeit.
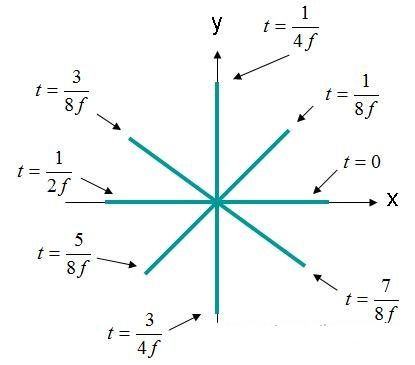
Abbildung 4. Elektrische Feldstärke (X, Y, Z) = (0,0,0) EQ-Bereich. (3).
Das elektrische Feld in Abbildung 4 rotiert kreisförmig. Diese Art von Feld wird als zirkular polarisierte Welle bezeichnet. Für eine zirkulare Polarisation müssen folgende Kriterien erfüllt sein:
- Standard für zirkulare Polarisation
- Das elektrische Feld muss zwei orthogonale (senkrechte) Komponenten aufweisen.
- Die orthogonalen Komponenten des elektrischen Feldes müssen gleiche Amplituden aufweisen.
- Die Quadraturkomponenten müssen um 90 Grad phasenverschoben sein.
Bei einer Bewegung entlang des Bildschirms in Abbildung 4 der Welle spricht man von einer Drehung des Feldes gegen den Uhrzeigersinn und von rechtszirkularer Polarisation (RHCP). Dreht sich das Feld im Uhrzeigersinn, ist es linkszirkular polarisiert (LHCP).
Elliptische Polarisation
Besitzt das elektrische Feld zwei zueinander senkrechte Komponenten, die um 90 Grad phasenverschoben, aber gleich groß sind, so ist das Feld elliptisch polarisiert. Betrachtet man das elektrische Feld einer ebenen Welle, die sich in +z-Richtung ausbreitet und durch Gleichung (4) beschrieben wird:
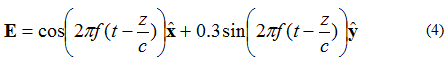
Der geometrische Ort des Punktes, an dem die Spitze des elektrischen Feldvektors ansetzt, ist in Abbildung 5 dargestellt.
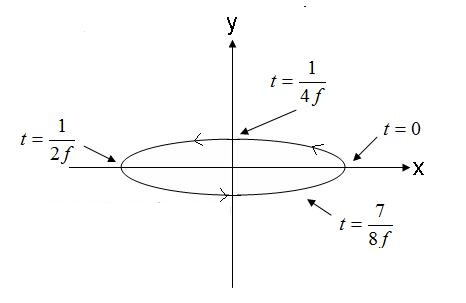
Abbildung 5. Elektrisches Feld einer prompten elliptischen Polarisationswelle. (4).
Das in Abbildung 5 dargestellte Feld, das sich entgegen dem Uhrzeigersinn ausbreitet, wäre rechtsdrehend elliptisch, wenn es aus der Bildebene herausginge. Dreht sich der elektrische Feldvektor in die entgegengesetzte Richtung, ist das Feld linksdrehend elliptisch polarisiert.
Elliptische Polarisation wird durch ihre Exzentrizität beschrieben. Diese entspricht dem Verhältnis der Exzentrizität zur Amplitude der Haupt- und Nebenachse. Beispielsweise beträgt die Wellenexzentrizität gemäß Gleichung (4) 1/0,3 = 3,33. Elliptisch polarisierte Wellen werden weiterhin durch die Richtung ihrer Hauptachse charakterisiert. Die Wellengleichung (4) hat eine Achse, die primär aus der x-Achse besteht. Die Hauptachse kann in jedem beliebigen Winkel in der Ebene liegen. Der Winkel muss nicht mit der x-, y- oder z-Achse übereinstimmen. Zirkulare und lineare Polarisation sind Spezialfälle der elliptischen Polarisation. Eine elliptisch polarisierte Welle mit einer Exzentrizität von 1,0 ist zirkular polarisiert. Elliptisch polarisierte Wellen weisen eine unendliche Exzentrizität auf. Linear polarisierte Wellen sind...
Antennenpolarisation
Nachdem wir nun polarisierte ebene elektromagnetische Wellenfelder kennen, lässt sich die Polarisation einer Antenne ganz einfach definieren.
Antennenpolarisation: Bei der Fernfeldbewertung einer Antenne wird die Polarisation des resultierenden abgestrahlten Feldes angegeben. Daher werden Antennen häufig als „linear polarisiert“ oder „rechtszirkular polarisierte Antennen“ bezeichnet.
Dieses einfache Prinzip ist wichtig für die Antennenkommunikation. Erstens kann eine horizontal polarisierte Antenne nicht mit einer vertikal polarisierten Antenne kommunizieren. Aufgrund des Reziprozitätstheorems sendet und empfängt die Antenne auf exakt dieselbe Weise. Daher senden und empfangen vertikal polarisierte Antennen vertikal polarisierte Felder. Versucht man also, eine vertikal polarisierte Antenne mit einer horizontal polarisierten Antenne zu verbinden, findet kein Empfang statt.
Im allgemeinen Fall zweier linear polarisierter Antennen, die um einen Winkel ( ) relativ zueinander gedreht sind, wird der Leistungsverlust aufgrund dieser Polarisationsfehlanpassung durch den Polarisationsverlustfaktor (PLF) beschrieben:
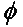
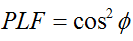
Wenn zwei Antennen die gleiche Polarisation aufweisen, beträgt der Winkel zwischen ihren abstrahlenden Elektronenfeldern null Grad, und es treten keine Leistungsverluste aufgrund von Polarisationsfehlanpassung auf. Ist eine Antenne vertikal und die andere horizontal polarisiert, beträgt der Winkel 90 Grad, und es findet keine Leistungsübertragung statt.
Hinweis: Das Bewegen des Telefons über dem Kopf in verschiedenen Winkeln erklärt, warum sich der Empfang manchmal verbessern lässt. Handyantennen sind üblicherweise linear polarisiert. Durch Drehen des Telefons kann die Polarisation oft an die des Telefons angepasst und somit der Empfang verbessert werden.
Zirkulare Polarisation ist eine wünschenswerte Eigenschaft vieler Antennen. Beide Antennen sind zirkular polarisiert und weisen keine Signalverluste aufgrund von Fehlanpassungen der Polarisation auf. Die in GPS-Systemen verwendeten Antennen sind rechtszirkular polarisiert.
Nehmen wir nun an, eine linear polarisierte Antenne empfängt zirkular polarisierte Wellen. Äquivalent dazu: Nehmen wir an, eine zirkular polarisierte Antenne versucht, linear polarisierte Wellen zu empfangen. Wie groß ist der resultierende Polarisationsverlustfaktor?
Zirkulare Polarisation besteht aus zwei orthogonal linear polarisierten Wellen, die um 90 Grad phasenverschoben sind. Daher empfängt eine linear polarisierte (LP) Antenne nur die Phasenkomponente der zirkular polarisierten (CP) Welle. Folglich weist die LP-Antenne einen Polarisationsfehlanpassungsverlust von 0,5 (-3 dB) auf. Dies gilt unabhängig vom Drehwinkel der LP-Antenne.
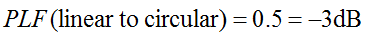
Der Polarisationsverlustfaktor wird auch als Polarisationswirkungsgrad, Antennenfehlanpassungsfaktor oder Antennenempfangsfaktor bezeichnet. Alle diese Bezeichnungen beschreiben dasselbe Konzept.
Veröffentlichungsdatum: 22. Dezember 2023







